Keep an eye: I think there are two versions of Maurer-Cartan form: for Lie groups and for principal bundles. Probably they can be seen like the same, considering the Lie group as a principal bundle over a point...

Maurer-Cartan form of a Lie group

UPDATED VERSION HERE

Given a Lie group $G$ with Lie algebra $g$ , we call (left-invariant) Maurer-Cartan form to the map:

θ_{g} := d (L_{g^{- 1}})_{g} : T_{g} G ⟶ T_{e} G ≅ g

for every $g \in G$ , and where $L_{g}$ denote the left-multiplication by $g$ . It is a $g$ -valued 1-form: $θ \in T^{*} G \otimes g$ . Its meaning is that identifies every $T_{g} G$ with $g$ (via left invariants vector fields), and so does with every two $T_{g} G$ and $T_{h} G .$ At this way, we have a sense of parallel transport.

Another point of view for Maurer-Cartan form:

Given a basis ${V_{i}}$ for $T_{e} G = g$ we can extend it to a global frame of $G$ by means of left translations (see examples here). Now, given $X \in T_{g} G$ , the components $μ_{i} (X)$ of $X$ in this frame are the Maurer-Cartan forms respect to the chosen basis. And the vector $μ_{i} (X) V_{i} \in g$ is also called the result of the Maurer-Cartan form. The individual Maurer-Cartan forms depend on the basis, but the "joint" one don't!

If the group is a matrix group then it can be computed with the expression $μ = g^{- 1} d g$ .

It is relevant for the method of moving frames.

Interpretation

See MC form for a matrix group#Interpretation.

Example

See example left invariants vector fields and Maurer-Cartan form.

MC form and left and right actions

What is the relation between left and right actions and the Maurer-Cartan form?

Suppose an element $g \in G$ . For a vector $V \in T_{e} G$ we have two vectors in $T_{g} G$ : the left translated ${\hat{V}}^{l} = d (L_{g})_{e} (V)$ and the right translated ${\hat{V}}^{r} = d (R_{g})_{e} (V)$ .

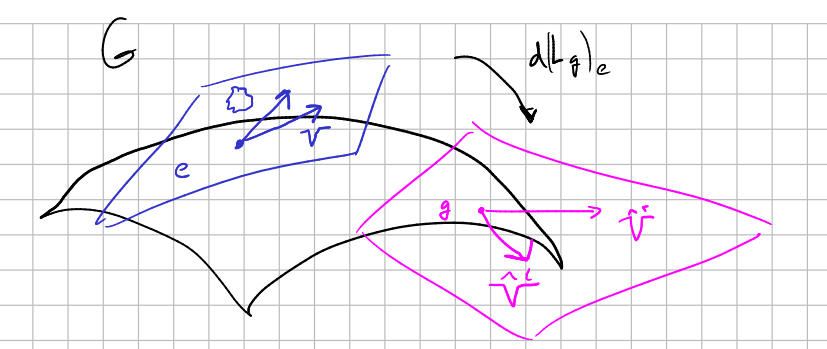
Since $d (L_{g})_{e}$ is a vector space isomorphism, we can wonder what vector in $T_{e} G$ corresponds to ${\hat{V}}^{r}$ be means of it, i.e., the vector $W$ such that:

d (L_{g})_{e} (W) = {\hat{V}}^{r} = d (R_{g})_{e} (V)

so obviously

W = (d (L_{g})_{e})^{- 1} d (R_{g})_{e} (V) = d (L_{g^{- 1}} \circ R_{g})_{e} (V) =

= A d_{g^{- 1}} (V),

the adjoint representation.

So since the Maurer-Cartan form $θ_{g}$ is an inverse for $d (L_{g})_{e}$ :

1. $θ_{g} \circ d (L_{g})_{e} = i d_{g}$

2. $θ_{g} \circ d (R_{g})_{e} = A d_{g^{- 1}}$

From 1 it can be deduced that

Proposition

The Maurer-Cartan form is a left-invariant differential form. Moreover, it is the only left-invariant form such that $θ_{e} = i d$ .

$◼$

Proof

Let $V \in T_{a^{- 1} g} G$ ,

L_{a}^{*} (θ_{g}) (V) = θ_{g} (((L_{a})_{*})_{a^{- 1} g} (V)) = θ_{g} (((L_{g})_{*})_{e} (θ_{a^{- 1} g} (V)) = θ_{a^{- 1} g} (V)

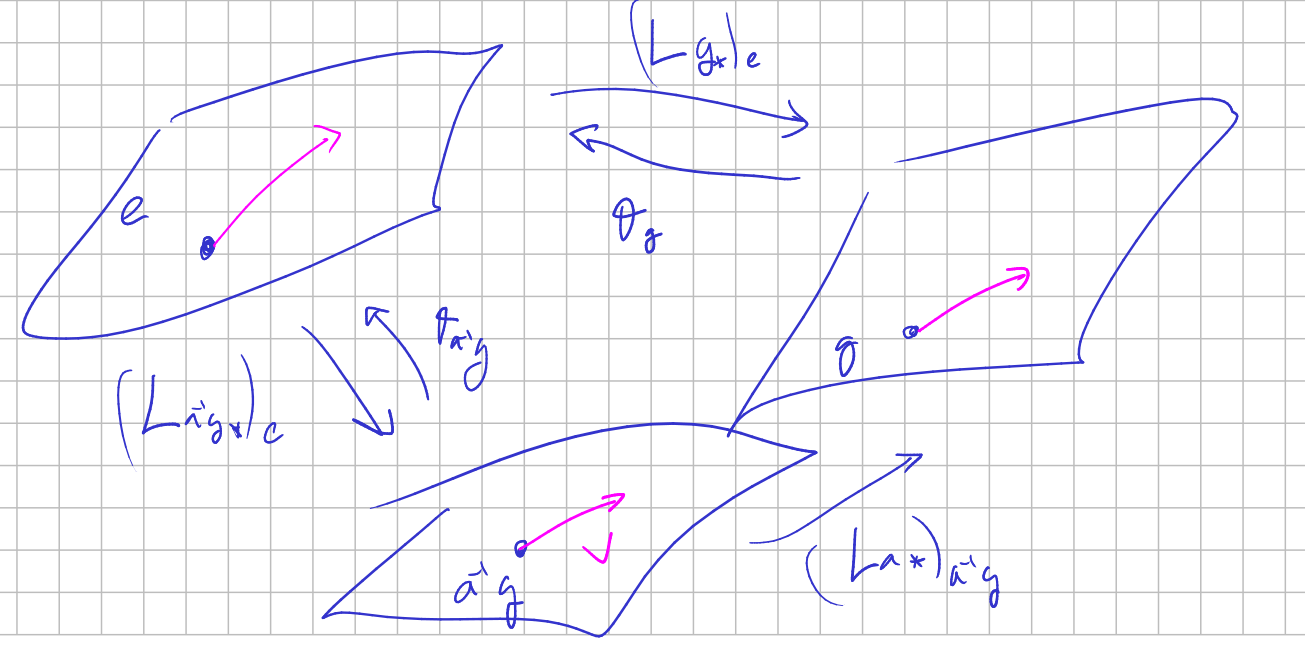
So it is left-invariant.

Now, if $α$ is another left-invariant 1-form with $α_{e} = i d = L_{g}^{*} (θ_{g})$ then

L_{g^{- 1}}^{*} (α_{e}) = L_{g^{- 1}}^{*} (L_{g}^{*} (θ_{g}))

and so

α_{g} = θ_{g} .

$◼$

From 2, we can write, treating $θ$ like a 1-form ( $g$ -valued):

\begin{matrix} (1) & R_{g}^{*} (θ) = A d_{g^{- 1}} θ \end{matrix}

for any $h \in G$ .

This can be seen from the following picture:

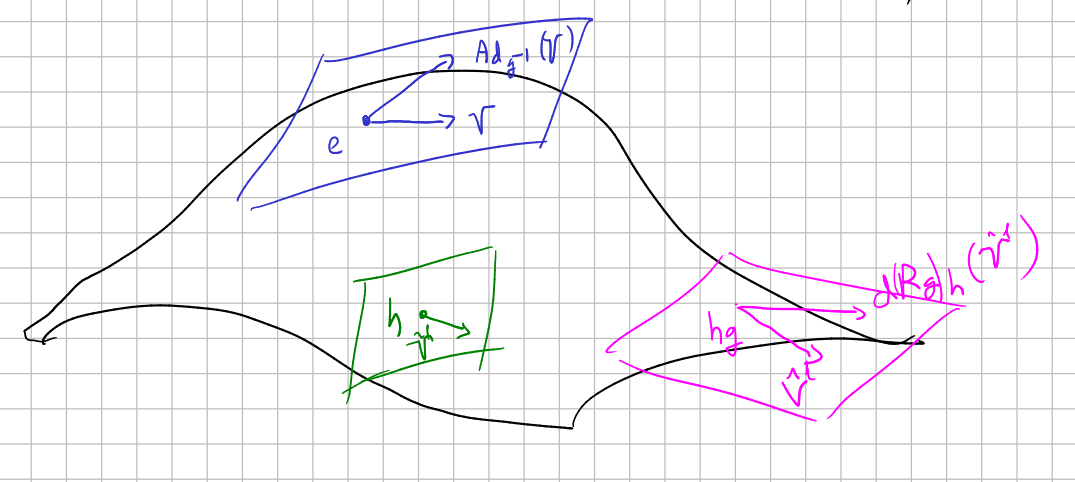
Let ${\tilde{V}}^{l} = d (L_{h})_{e} (V) \in T_{h} G$ (it could have been an arbitrary $W \in T_{h} G$ , but I found more visual this way). The right hand side of (1) would be telling to us that

{\tilde{V}}^{l} \overset{θ_{h}}{⟼} V \overset{A d_{g^{- 1}}}{⟼} A d_{g^{- 1}} (V)

and the left hand side:

{\tilde{V}}^{l} \overset{d (R_{g})_{h}}{⟼} d (R_{g})_{h} ({\tilde{V}}^{l}) \overset{θ_{h g}}{⟼} A d_{g^{- 1}} (V)

But that would be true if $d (R_{g})_{h} ({\tilde{V}}^{l}) = d (R_{h g})_{e} (V)$ , but this is true because

d (R_{g})_{h} ({\tilde{V}}^{l}) = d (R_{g})_{h} (d (L_{h})_{e} (V)) = d (R_{g} \circ L_{h})_{e} (V) =

= d (R_{h g})_{e} (V)

Keep an eye: I am not sure about how to proof the last equality, but it must be true...

On the other hand, the Maurer-Cartan form

Structural equation/MC equation

Given a Lie group $G$ with Lie algebra $g$ , the Maurer-Cartan form satisfies the following condition

d θ (X, Y) + [θ (X), θ (Y)] = 0

where $X, Y$ are vector fields (any) on $G$ . It is called also the Maurer-Cartan equation.

It is also written

d θ + \frac{1}{2} [θ, θ] = 0

for a Lie bracket defined in this way: If $ω, θ$ are two $g$ -valued 1-forms, define the $g$ -valued 2-form $[ω, θ]$ by

[ω, θ] (X, Y) = [ω (X), θ (Y)] + [ω (Y), θ (X)] .

Proof

See [Sharpe 1991] page 108. $◼$

It is similar to the curvature of a principal connection. Indeed, this structural equation is saying that a Klein geometry is a flat Cartan geometry. To see in what sense this is a kind of generalization of curvature (zero curvature, indeed) see Generalization of the flatness of R3.

Maurer-Cartan form on a principal bundle

Suppose $P \to M$ is a $H$ -principal bundle. Then, given $v \in h$ we can consider the fundamental vector field $v^{♯}$ . For $p \in P$ , $v_{p}^{♯}$ is a vertical vector since the action of $G$ leaves the fibres invariant. So for every $p$ we have a linear isomorphism (need to be proven)

\begin{array}{rcl} i_{p} : h & \to & V_{p} P \subseteq T_{p} P \\ v & \to & v_{p}^{♯} = \frac{d}{d t} |_{t = 0} (p \cdot e^{t v}) \end{array}

The inverse $(i_{p})^{- 1}$ , is like a Maurer-Cartan form, which acts only on vertical vector fields. That is, we can define a kind of $h$ -valued 1-form $θ^{P}$ by

θ_{p}^{P} (V) = v

where $V = \frac{d}{d t} |_{t = 0} (p \cdot e^{t v}) \in V_{p} P$ , linear.

In the particular case of a Klein geometry seen as a principal bundle, the Maurer-Cartan form on the principal bundle in the sense described in this subsection coincides with the one of the beginning. See here for details.

(By the way, I think that giving a connection to $P$ is "the same as" extending this 1-form $θ^{P}$ to any vector, not only the vertical ones. In the case of a Cartan connection we are doing the same, but the values are taken in an extended Lie algebra...)

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es

INDEX: